Interprétation géométrique. Soit la fonction y = ¦ (x) définie et dérivable dans l’intervalle (a, b). Soit C son graphe par rapport à deux axes de coordonnées Ox et Oy rectangulaires ou obliques. Soit x₀ une valeur fixe et x une valeur variable de (a, b), M₀ et M les deux points distincts de C d’abscisses x₀ et x. La droite M₀M a pour coefficient directeur .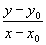

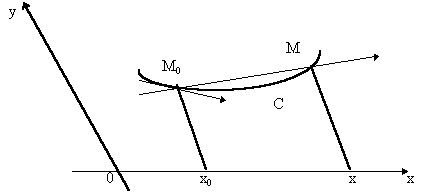
Fig. 1.

Si on fait tendre x vers x₀, M tend vers M₀ sur C, le rapport 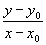 tend par hypothèse vers la dérivée  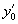de la fonction pour x₀. La droite M₀M, qui pivote autour de M₀, tend donc vers une position limite M₀T dont le coefficient directeur est .

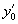Par définition M₀T est la tangente à C en M₀.

Théorème. Soit une fonction définie et dérivable dans l’intervalle (a, b); en tout point de son graphe, elle admet une tangente dont le coefficient de direction est la valeur de la dérivée en ce point.

Remarques. 1⁰  Si 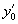 = 0 la tangente en M₀ est parallèle à O_x.

 
2⁰  Si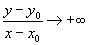 
(ou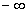) lorsque  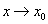par valeurs supérieures et inférieures, la courbe admet au point M₀ une tangente parallèle à O_y. 

Nous admettons sans démonstration que:

Théorème. Soit une fonction dérivable sur l’intervalle (a, b) ouvert ou fermé.

1⁰ Si la dérivée est nulle 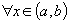, la fonction est constante.

2⁰ Si la dérivée est positive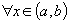, la fonction est croissante.

3⁰ Si la dérivée est négativ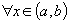e, la fonction est décroissante.

Application. Pour étudier le sens de variation d’une fonction dérivable y = ¦ (x) on calcule la fonction dérivée. L’étude de son signe permet de décomposer l’intervalle (a, b) en intervalles partiels. Dans chacun de ceux-ci la dérivée a un signe constant, et on applique le théorème précédent.