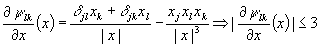Lemme 1 (i) A est maximal monotone
(ii) F est localement lipchitzienne de X dans X
Démonstration: (i) Il suffit de montrer que A + 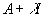est,
pour tout ,
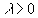surjectif de D(A) dans X. Ceci se montre aisément à l’aide
du théorème de Lax - Milgram et de l’injection continue .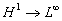
La difficulté essentielle réside dans la démonstration
du fait que l’application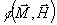
est localement lipchitzienne de
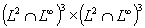dans .
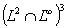On vérifie aisément que l’on est ramené à étudier
le caractère lipchitzien des fonctions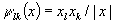
de R3 dans ,
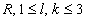ce qui se déduit du fait que les fonctions 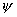sont
presque partout dérivables, à gradient borné:
est,
pour tout 
,
surjectif de D(A) dans X. Ceci se montre aisément à l’aide
du théorème de Lax - Milgram et de l’injection continue 
.
est localement lipchitzienne de 
dans 
.
On vérifie aisément que l’on est ramené à étudier
le caractère lipchitzien des fonctions 
de R3 dans 
,
ce qui se déduit du fait que les fonctions 
sont
presque partout dérivables, à gradient borné:
