Entiers naturels
Ainsi sont appelés les nombres entiers positifs 1, 2, 3, 4,
... L’ensemble de ces nombres est noté (1) N*. Lorsqu’on y
inclut le nombre zéro, on le note N.
Nombres premiers
Un nombre entier positif est dit premier s’il n’est divisible
que par 1 et par lui-même . Par exemple 3, 5, 67, 103 sont
des nombres premiers. Tout entier positif peut s’écrire de façon
unique comme un produit de nombres premiers. Par exemple: 504 = 23´3²´
7.
Entiers
Lorsqu’on adjoint un signe "moins" aux entiers naturels, on obtient
les entiers négatifs (-1, -2, -3, etc.). Avec les entiers naturels,
ils constituent l’ensemble des entiers (..., -3, -2, -1, 0, 1, 2, ...).
Cet ensemble, dit aussi des "entiers relatifs", est noté
Z.
Nombres rationnels
Il s’agit des nombres qui peuvent s’écrire comme un rapport
de deux entiers, c’est-à-dire comme une fraction.
En d’autres termes, un nombre rationnel peut s’écrire sous la
forme p/q, où p et q sont des entiers (l’écriture n’est pas
unique). Par exemple 1/2, -2/3, 8/9 = 16/18, 6/2 = 3/1 = 3 sont des nombres
rationnels.
L’ensemble des nombres rationnels est désigné par
Q. L’ensemble Z des entiers en est un sous-ensemble.
Le développement décimal d’un nombre rationnel comporte
toujours un groupe de chiffres (éventuellement un seul chiffre)
qui se répète infiniment, à partir d’un certain
rang. Par exemple, 23,0215454545454.... est le développement décimal
de 253 237/11 000.
Nombres irrationnels
Ce sont les nombres dont le développement décimal
est infini et non périodique. Ils ne peuvent donc pas s’écrire
comme un rapport d’entiers. Par exemple, 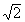 =
1,4142 .... est irrationnel, comme l’avaient prouvé les Pythagoriciens.
Autres exemples d’irrationnels: p ,
=
1,4142 .... est irrationnel, comme l’avaient prouvé les Pythagoriciens.
Autres exemples d’irrationnels: p , 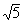 ,
1 +
,
1 + 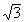 , etc.
De fait, la plupart des nombres sont irrationnels. Leur infinité
est en effet d’un ordre supérieur à celle des nombres
rationnels. Par ailleurs, la plupart des irrationnels sont aussi transcendants.
, etc.
De fait, la plupart des nombres sont irrationnels. Leur infinité
est en effet d’un ordre supérieur à celle des nombres
rationnels. Par ailleurs, la plupart des irrationnels sont aussi transcendants.
Nombres réels
L’ensemble des nombres réels réunit l’ensemble des rationnels
et l’ensemble des irrationnels; il est noté R.
L’ensemble R a été rigoureusement "construit" durant
la deuxième moitié du XIXe siècle par diverses
méthodes. Plusieurs mathématiciens y ont contribué
(le Français Charles Méray, les Allemands Karl Weierstrass,
Richard Dedekind et Georg Cantor, etc.). Dans la méthode de Cantor,
on considère des suites d’éléments de Q (c’est-à-dire
de nombres rationnels) possédant une certaine propriété
technique (il s’agit des "suites de Cauchy"). Un exemple est
la suite de nombres rationnels 1, 1 -1/3, 1 -1/3 + 1/5, 1 -1/3 + 1/5
-1/7, etc. Cette suite converge vers le nombre 0,78539816.... (qui
est égal à p /4). La limite d’une
telle suite de rationnels n’est pas toujours un nombre rationnel, comme
le montre cet exemple. Mais on peut définir sur ces limites les
mêmes opérations (addition, multiplication, etc.) qui
ont cours sur les nombres rationnels. L’ensemble des nombres réels
est alors obtenu en "complétant" l’ensemble Q avec les limites
de suites convergentes de nombres rationnels. Ainsi construit , l’ensemble
R comprend les nombres rationnels et les nombres irrationnels (lesquels
sont, grâce à cette construction, bien définis), et
permet par ailleurs de décrire tous les points d’une droite: à
tout point d’une droite on peut associer un nombre réel et un seul,
et réciproquement.