Soient ¦ une fonction
définie sur un intervalle ouvert I et x0 un point de
I. La fonction ¦ est dérivable
en x0 si le rapport
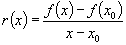
a une limite à gauche finie et une limite à droite
finie en x0 et si ces deux limites sont égales.
Cette
limite commune est le nombre dérivé de
¦
en x0, noté 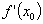 : :
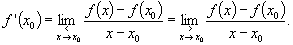
La fonction ¦ est dérivable
(1) à droite en x0 (resp. dérivable
(1) à gauche en x0) si le rapport r (x) a une
limite à droite finie (resp. à gauche) en x0.
Cenombre
dérivé à droite (resp. à gauche)
est noté
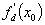 (resp. (resp. 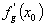 ). ).
Si une fonction est dérivable (1) en x0, alors
elle est dérivable (1) à gauche et à droite
en x0.
Attention, une fonction peut être dérivable (1)
à gauche et à droite en x0 sans être dérivable
(1) en x0.
Si une fonction est dérivable en x0, alors
elle est continue en x0.
On peut étendre de manière évidente la notion de dérivée
à droite dans le cas de la borne a d’un intervalle [a, b[et de
même la notion de dérivée à gauche en b
dans le cas d’un intervalle]a, b].
La fonction 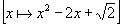 est dérivable en 1 de nombre dérivé 0.
La fonction ¦ définie sur R par
est dérivable en 1 de nombre dérivé 0.
La fonction ¦ définie sur R par 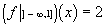 et
et 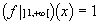 est
dérivable
(1) à gauche en 1 mais pas à droite.
La fonction g définie sur est
dérivable
(1) à gauche en 1 mais pas à droite.
La fonction g définie sur 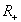 par
par 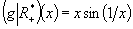 et
g(0) = 0 est continue en 0, mais n’est pas dérivable (1)
à droite en 0.
La fonction h: et
g(0) = 0 est continue en 0, mais n’est pas dérivable (1)
à droite en 0.
La fonction h: 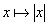 est dérivable (1) à gauche et à droite en 0,
mais
n’est pas dérivable en 0.
est dérivable (1) à gauche et à droite en 0,
mais
n’est pas dérivable en 0.
Si ¦ est dérivable (1)sur
I, c’est-à-dire en tout point de I, la fonction dérivée,
notée ¦‘, est l’application
qui
fait correspondre à tout élément x de I le nombre
dérivé de ¦ en x.
La fonction dérivée de la fonction sin est la fonction cos.
|