Considérons une équation sous forme normale:

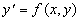
(1)

où ¦ est définie sur un ouvert W de R².

Soit (1) G le graphe d’une fonction 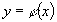 définie sur un intervalle ouvert I. Pour que ce soit (2) un arc intégral de l’équation (1), il faut et il suffit qu’il soit (3) contenu dans W et qu’il possède, en tout point m = (x, y) une tangente d de pente .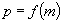

On dit que le couple (m, d ) est un élément de contact de l’arc G .

D’une façon générale, on appelle élément de contact (dans R²) tout couple 

(m, d ) formé d’un point m de R² et d’une droite d passant par m. Ce point est le support de l’élément de contact.

Etant donné un domaine quelconque W de R² un champ d’éléments de contact de supportW est un ensemble C d’éléments de contact tel que tout point m de Wsoit (4) le support d’un élément de C et d’un seul.

Revenons alors à l’équation (1). Si l’on associe à chaque point m de 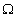 la droite d de pente 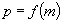qui passe par m, on obtient un champ C d’éléments de contact. Réciproquement,si C est un champ d’éléments de contact ayant pour support un ouvert 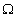, et tel que la pente 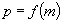 de chacune de ses droites soit (4) finie, on peut considérer qu’il est défini par l’équation différentielle .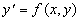

D’après ce que nous avons observé plus haut, le graphe G d’une fonction 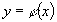 définie sur un intervalle ouvert I est un arc intégral de l’équation (1) si et seulement s’il possède une tangente de pente finie en chaque point et si tous ses éléments de contact appartiennent au champ C associé à l’équation (1).

Cette interprétation du problème de l’intégration de l’équation (1) lui (6) confère un aspect géométrique qui est souvent utile, soit (5) pour trouver des solutions, soit pour découvrir des propriétés intéressantes des intégrales de l’équation envisagée.