Texte 5

Calcul différentiel. Extremums locaux

     
  • La fonction dont (1) le graphe est représenté sur la fig. 1 admet six extremums locaux stricts dont (1) deux sont globaux.

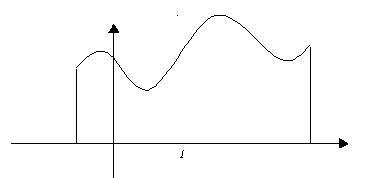
Figure 1: Extremums locaux

Si la fonction est dérivable, on a une condition nécessaire pour avoir un extremum local:
Soient ¦une fonction dérivable sur un intervalle ouvert I et x0 un point de I. Si ¦ admet un extremum local en x0, alors ¦¢ (x0) = 0.
  • Attention, cette condition n’est pas suffisante: il se peut que la dérivée s’annule sans qu’il y ait (2) un extremum local. Par exemple, la fonction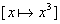, définie sur[-1,1], n’admet pas d’extremum local en 0, bien que sa dérivée s’annule (3) en 0.
  • Soit ¦ une fonction définie sur [a, b]. Il est possible que ¦ admette (4) un extremum en a ou b sans que ¦¢ (a) ou ¦¢ (b) soit (2) nul. Par exemple, la fonction ¦ : 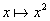 définie sur [0, 1] admet un maximum en 1, mais .
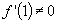    • La fonction 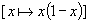, définie sur [0, 1] admet un maximum global (strict) au point 1/2. On a donc l’inégalité
.
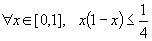A l’aide de cette condition nécessaire, on démontre le résultat suivant:
Théorème de Rolle. Soit ¦ une fonction définie sur un segment [a, b] (avec a < b), dérivable sur l’intervalle ouvert ]a, b[, et telle que ¦ (a) = ¦ (b). Alors, il existe un élément c de ]a, b[ tel que ¦¢ (c) = 0. 










exercices